Inada-type condition
WebIn macroeconomics, the Inada conditions (named after Japanese economist Ken-Ichi Inada) are assumptions about the shape of a production function that guarantee the stability of an economic growth path in a neoclassical growth model. The six conditions for a given function are: the value of the function at 0 is 0: the function is continuously ... In macroeconomics, the Inada conditions, named after Japanese economist Ken-Ichi Inada, are assumptions about the shape of a function, usually applied to a production function or a utility function. When the production function of a neoclassical growth model satisfies the Inada conditions, then it guarantees the … See more The elasticity of substitution between goods is defined for the production function $${\displaystyle f(\mathbf {x} ),\mathbf {x} \in \mathbb {R} ^{n}}$$ as In stochastic neoclassical growth model, if the production … See more • Barro, Robert J.; Sala-i-Martin, Xavier (2004). Economic Growth (Second ed.). London: MIT Press. pp. 26–30. ISBN 0-262-02553-1 See more
Inada-type condition
Did you know?
WebThe Inada surname appeared 248 times in the 2010 census and if you were to sample 100,000 people in the United States, approximately 0 would have the surname Inada. … Web1 day ago · On April 12, 2024, Jamie Foxx’s daughter Corinne Foxx issued a statement on her Instagram. “We wanted to share that my father, Jamie Foxx, experienced a medical complication yesterday,” the ...
WebThere are two corresponding Inada conditions for labor. The first of these is: For all K ∈ R++, lim L→∞ FL(K,L)=0 [IL→∞] (5) Analogous to (2) we say that capital is essential if the … WebThis Chapter provides a characterization of strict majority rule and Inada-type necessary and su cient conditions for transitivity and quasi-transitivity under the strict majority rule. Under the strict majority rule, also called non-minority rule, an alternative x is considered to be socially at least as good as some other alternative y
WebJul 1, 2024 · Clearly, the Inada type conditions are assumed to obtain interior solution. The last assumption is necessary to use implicit function theorem. Clearly, both are satisfied e.g. by a power utility function. The next remark discusses the class of stochastic transitions that satisfy our conditions. Remark 1 WebTransversality Conditions and ... This can be ensured by the Inada condition mentioned above. The first order condition with respect to x t+1 remains the same, ... in money-in-the-utility-function models of the type studied by Brock (1974) and Obstfeld and Rogoff (1986). In these models, agents derive utility from ...
WebIn macroeconomics, the Inada conditions (named after Japanese economist Ken-Ichi Inada) are assumptions about the shape of a production function that guarantee the stability of an economic growth path in a neoclassical growth model.. The six conditions for a given function are: the value of the function at 0 is 0: the function is continuously differentiable,
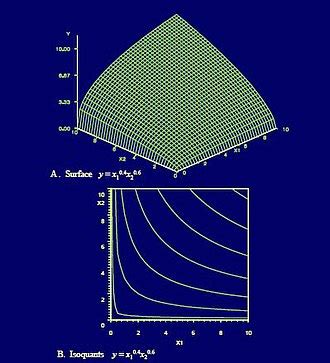
http://www.sef.hku.hk/~wsuen/ls/immortal/i2.html open mouth imageWebThere are many non Cobb-Douglas functions that satisfy the Inada conditions, albeit they may not have nice compact formulas. E.g., f ( x) = { x 1 / 2 if x ≤ 1 2 x 1 / 4 − 1 if 1 < x This … ip address of cg netWeb稲田条件(英: Inada conditions)とは、マクロ経済学における新古典派成長モデルの生産関数に関する仮定である。 経済の成長経路が安定的になることを保証する。 日本の経済学者の稲田献一にちなんで名付けられた[1]。 宇沢弘文により、この条件が導入された[2]。 与えられる関数f(x){\displaystyle f(x)}は以下の6つの条件を満たす。 関数 f(x){\displaystyle … ip address of brother printer mfc 8810dwWeban Inada-type necessary and sufficient condition for quasi-transitivity is that the Latin Square partial agreement holds over every triple of alternatives. (iv) When the number of individuals is four, an Inada-type necessary and sufficient condition for quasi-transitivity is that the weak extremal restriction holds over every triple of ... ip address of cs 1.6WebIn macroeconomics, the Inada conditions (named after Japanese economist Ken-Ichi Inada) are assumptions about the shape of a production function that guarantee the stability of … ip address of cell phoneWebMerton's theorem on the existence of a steady state with Inada-type production functions. The existence and uniqueness gap in the literature is partly attributed to the fact that Ito's theorem on the existence and uniqueness of the solution to a given stochastic differential equation cannot be directly applied because the stochastic Solow equation open mouth illustrationWebApplicability of Ind AS 115 is postponed. In a relaxation that will provide immense relief to India Inc, which was grappling with the complexities of the new accounting standard on … open mouth kissing hiv